puzzle9-problem

发表于 | 分类于 ，

1.The 9 puzzle描述
2.代码分析部分
3.延伸N宫格

The 9 puzzle描述

Dispatch the integers from 0 to 8, with 0 possibly changed to None, as a list of 3 lists of size 3, to represent a 9 puzzle.

For instance, let [[4, 0, 8], [1, 3, 7], [5, 2, 6]] or [[4, None ,8], [1, 3, 7], [5, 2, 6]] represent the 9 puzzle


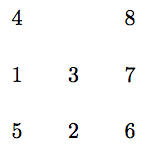
with the 8 integers being printed on 8 tiles that are placed in a frame with one location being tile free.

The aim is to slide tiles horizontally or vertically so as to eventually reach the configuration

It can be shown that the puzzle is solvable iff the permutation of the integers 1, …, 8, determined by reading those integers off the puzzle from top to bottom and from left to right, is even. This is clearly a necessary condition since:

  • sliding a tile horizontally does not change the number of inversions;

  • sliding a tile vertically changes the number of inversions by -2, 0 or 2;

  • the parity of the identity is even.

Complete the program nine_puzzle.py so as to have the functionality of the two functions:

  • validate_9_puzzle(grid) that prints out whether or not grid is a valid representation of a solvable 9 puzzle

  • solve_9_puzzle(grid) that, assuming that grid is a valid representation of a solvable 9 puzzle, outputs a solution to the puzzle, with a minimal number of moves.

代码分析部分


这道题其实就是判断给定九宫格是否是合法的，并且是可求解的。
如果是可以求解的，就求解。

对于是否合法，如果存在None，置换为0，如果不是1-8的数字和0/None构成，则不成立。
接下来判断是否有解，使用这段代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# sum为奇数时return
        if sum(1 for i in range(8) for j in range(i + 1, 9) if grid[i] and grid[j] and grid[i] > grid[j]) % 2:	
		    return

``` 
之后就是寻找该解，使用队列进行操作。
用来存放可以移动的位置，例如，如果0为空，只能移动1和3。

``` python3
        # 0 1 2
        # 3 4 5
        # 6 7 8
        neighbouring_cells = {0: {1, 3}, 1: {0, 2, 4}, 2: {1, 5},
                              3: {0, 4, 6}, 4: {1, 3, 5, 7}, 5: {2, 4, 8},
                              6: {3, 7}, 7: {4, 6, 8}, 8: {5, 7}
                              }
``` 

以下为关键代码，遍历每一种可能性，对于每一种可能，继续延伸。如果不在已经看过的grid中，就加入直到有一个队列，最终和目标一致。输入这个过程。

``` python3
        while True:
            game = games_queue.popleft()
            grid, empty_cell = game[-1]
            if grid == target_grid:
                break
            for new_empty_cell in neighbouring_cells[empty_cell]:
                new_grid = list(grid)
                new_grid[empty_cell], new_grid[new_empty_cell] = \
                    new_grid[new_empty_cell], new_grid[empty_cell]
                new_grid = tuple(new_grid)
                if new_grid not in seen_grids:
                    new_game = game + [(new_grid, new_empty_cell)]
                    games_queue.append(new_game)
                    seen_grids.add(new_grid)

判断可解的复杂度是O(N)

延伸N宫格


对于N宫格来说，判断是否有解。主要是判断反转(disorder)的个数。
反转：对于每一个格子来说，指的是在他之后（也就是从上到下,从左到右）的拥有更低的数字的格子。

对于奇数的盘，例如33的9宫格，则只需要判断反转数是否为奇数。为奇数，则有解。
对于偶数的盘，例如44的16宫格，需要判断反转数以及空格子的行数的和是否是偶数。为偶数，则有解。

最简单的算法也就是O(N^2),也就是上面的python代码。之后我用C写了一个O(NlogN)的，利用了归并排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int mergeSort(int *arr,int size,int left,int right){
	int disorder = 0;
	//to store the sorted arr
	int *temp = (int*)malloc(size*sizeof(int));
	if(left < right){
		int mid = (left + right)/2;
		disorder += mergeSort(arr,size,left,mid);
		disorder += mergeSort(arr,size,mid+1,right);
		disorder += merge(arr,temp,left,mid,right,size);		
	}
	free(temp);	
	return disorder;	
}

int merge(int *arr,int *temp,int left,int mid,int right,int size){
	int i = left;
	int j = mid+1;
	int k =left;
	int disorder = 0;	
	while(i <= mid  && j <=right){
		if( *(arr+i) < *(arr+j)){
			*(temp + k++) = *(arr+i);
			i++;
		}
		else{
			*(temp +k++) =*(arr+j);
			j++;
			disorder += mid+1-i;
		}
		
	}
	while(i<=mid){
		*(temp + k++) = *(arr+i);
		i++;
	}
	while(j<=right){
		
		*(temp +k++) =*(arr+j);
		j++;
	}	
	return disorder;	
}

具体思路：由于每次归并，都是排好序的，所以当如果有个格子的左边比右边大时，在这个左边格子的之后所有格子都比右边要大，因此就可以计算出反转的个数。

Jie wechat
学就完事